Multiple Response Optimization with Design of Experiments (DOE)

 

Design of experiments, is a systematic experimentation, with a process critical factors, in order to correlate these factors to process responses.

In DOE with Excel we obtained a linear relationship, between several factors and one response. 

In Response Surface DOE this was extended to non-linear relations.

In both cases we were optimizing one single response. Now we will analyse some cases where more than one response needs to be optimized.


Problem Description

Download file Multiple Response.xlsm from OneDrive to your PC.

We want to maximize yield and minimize cost in a process where we have identified three critical factors which may affect both.

These are the factors and levels we want to experiment with:




Full Factorial DOE

We start with a full factorial with two central points DOE and run a simulation of the experiments in sheet YieldCost Simul  we then add the interaction columns (green headers) for the analysis:


We now use Excel Data Analysis > Regression to analyse Yield:


 And the result in sheet Factorial is:


Same with Cost and we obtain:


In both cases R Square is not so good (0.72 and 0.63) and all p-values are above 0.05 so this model is not acceptable. 
We will now use a Pivot Chart to see the influence of pH on Yield:


The central point is not in line with the extreme values of +1 and -1 so this is an indication of curvature: the linear model is not valid. 
So we will do a response surface DOE for 3 factors. We will select the CCI design to avoid using pH values beyond the physically possible values (sheet RSMdesigns).
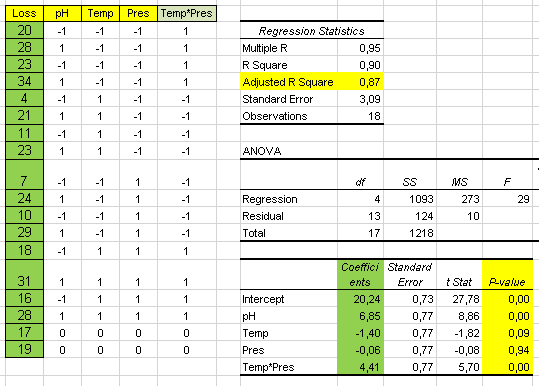
We run the experiments in the simulator YieldCost Simul and then add factor quadratic terms and interactions:


The result of the regression analysis in sheet RSMresult for yield and cost is:


Much better R Square values. We now remove non-significant terms and repeat the analysis (sheet Reduced):


The resulting formulas:

Yield = 31 + 101 pH + 45 Time - 99 pH*pH - 52 Time*Time
         
Cost = 45 - 19 pH + 21 Time + 45 pH*pH + 39 Time*Time

We prepare for SOLVER to optimize:


We will ask Solver to place the pH and Time values we are looking for in T18 anf T19

In T17 we put the value 1 which will multiply with Intercept to leave it as it is

In T20 we put the formula "=T18*T18" to calculate pH^2

In T21 the formula "=T19*T19" to calculate Time^2

In I22 the formula "=SUMPRODUCT(I17:I21,T17:T21)" to calculate yield as a function of the coefficients and the values of pH and Time

In O22 the formula "=SUMPRODUCT(O17:O21,T17:T21)" to calculate cost

We will start by maximizing Yield:

With the result:


We can maximize yield to a value of 66.9 with a cost of 63.8 with the coded values of pH = 0.51 and Time = 0.44

We can decode these values in sheet Decoding:




That is pH = 9.55 and Time = 12.76


If we minimize Cost:
It's at the expense of a large drop in Yield.

If we maximize Yield with a maximum Cost of 50:



Recap:


Confirmation Runs

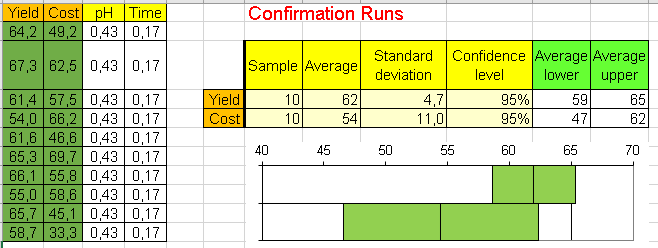
We will now run 10 confirmation runs (sheet Confirmation) with our estimated ideal pH and Time values (coded):


These are the confidence intervals for Yield and Cost corresponding to these ideal values of pH and Time.

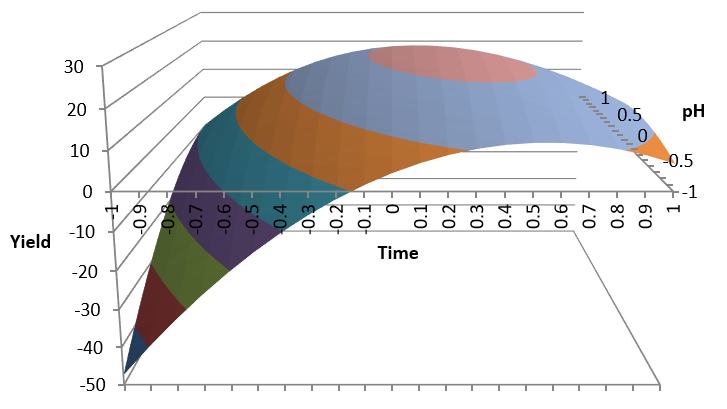
Response Surface Graphics

Since we only have two significant factors in this case (pH and Time) we can draw the response surfaces corresponding to our estimated formulas:

Photolitography Process

Let us now analyse another example.
We want to meet the following response specifications:




By adjusting the following critical factors:




So we have run Response Surface CCI experiments and added quadratic and interaction terms for the analysis (Sheet PHOTO):


The analysis results for the three responses (sheet PHOTOanalysis):


We now prepare for Solver:


For each response we only select those factors and interactions which are significant (p < 0.05)

We need Solver to calculate the values for the factors in the yellow cells (AI15-AI17)

These factor values should be between +1 and -1

We specify the max and min values required in the responses

We select response EDGE to be maximized as well as meet the min restriction of 3.

Solver was able to find factor values that meet all specifications.

Conclusions

  • Design of experiments could be extended to non-linear relations between factors and responses
  • In some occasions more than one response needs to be optimized
  • Excel data analysis regression can be used to approximate a mathematical formula to each of the responses
  • Excel Solver is useful to optimize the process, meeting multiple factor and response restrictions 
  • Several alternatives can be easily analysed with Solver once the mathematical model has been validated















Comments

Post a Comment

Popular posts from this blog

Design of Experiments (DOE) with Excel

Image
Design of Experiments (DOE) is a very useful process improvement methodology.  Microsoft Excel has some powerful data analysis tools, which I have, successfully, used for DOE. When it comes to analyzing cause and effect, we want to know what process factors affect our outputs.   Correlation and Regression could give us an indication of the main factors, and the extent they affect the outputs. In some cases, there may be interactions among the different factors, or the mathematical relation between factors and outputs may not be linear. In these cases, it is useful to run a systematic set of experiments, to test all possible combinations of factors, to relate them to the outputs. Factorial Experiment Example We want to minimize process loss, and after some brainstorming among the process specialists, we concluded that 5 factors may affect loss. Based on current factor levels, we have selected the following levels to experiment with:    Download this Excel file DOE_w...
Read more

Response Surface Design Of Experiments with Excel

Image
Design of Experiments is a useful methodology for process improvement. The purpose is to find a relationship between process variables we can control and key process outputs in order to increase process capability . You can use Excel statistical analysis tools, Solver, Pivot charts, etc. to plan and analyse the results of these experiments. The first approach is to look for a linear relationship as shown in:   Excel DOE But in some cases this relationship may not be linear, in which case we will try a quadratic model with Response Surface DOE . We will use an example in this Excel file you can download: Download file   ExcelResponseSurface.xlsm   from OneDrive to your PC. In this example we are trying to maximize process yield acting on the critical factors pH , Temperature and Time . We will run the experiments in the Experiments simulation sheet using coded values.   Code pH Temperature Time -1 2 120 7 1 12 150 15 Factorial Experiments We start by ru...
Read more

Virtual Obeya Room

Image
The Obeya room is a "war room" used by process improvement teams to meet and solve critical multi functional problems.  The room walls are lined up with boards, highly visual charts and graphs showing program timing, milestones and progress to date and countermeasures to existing timing or technical problems.  The team meets in this room regularly but team members can also visit the room, which is fully dedicated to the project, throughout the day. What is an Obeya? Obeya Room Benefits Remove organizational barriers Visual management by displaying all relevant data required in the improvement project Encourage a collaborative environment through regular meetings Implement quicker, more effective solutions The whole team knows what is going on in real time Some Practical Constraints in the Implementation Some companies can't afford the luxury of a fully dedicated room Some of the team members may be located far away so they will only attend the meetings The data displayed ...
Read more