Autocorrelation: How to Manage it


When a process variable has only random variation, each output is independent of the previous ones.This is what happens in a lottery.

In some processes this independence does not happen.
 
If we control our daily weight, for instance, our weight today is correlated to the weight of the previous days: it has autocorrelation.


Weight Autocorrelation

One common case of autocorrelation is shown by our body weight. 

Our weight today is correlated with:

Yesterday's weight:    53%

The day before:          39%  

Body weight has inertia: you don't expect sudden changes.

A similar effect happens when you control a heavy aircraft or a ship: its masive weight prevents you from making a sharp turning or make a sudden stop. 

This opposing force to change is what is called Inertia.

This inertia definition applies to moving objects and it is proportional to the object mass. 

Inertia also applies to fluids: a tank accumulating a fluid will also have this inertia effect.

If we try to control a process, which only has  random variation, by reacting to every output, we can see in Dice throwing Exercise that the process will get worse: variation will increase. This is a case of over-reaction.

We will see another instance of over-reaction caused by process inertia.


Airplane Tilt Control

We will now experience how to control a process with inertia, with a simulator of the tilt control in an airplane:


Download this Excel file Inertia simulator.xlsm from OneDrive.

Close other Excels and allow macros to run it.

Press Start to start simulating.

Move the cursor Up/ Down to adjust the tilt (do not click).

You should try to keep tilt as close to zero as possible.

The graphs below will show you the adjustments you made and the actual tilt evolution along 50 runs.

The Average and StdDev on top will tell you the extent of your success: you want both to be minimal.


Tilt Reduction by Adjusting

We have produced the following results after 50 runs:


We experienced the difficulty of reacting to this random behavior. 

We notice there is a delay in the response which drives us to over-adjust.

The histogram of the actual tilt evolution is:


It is normal with an average of 1.47 and a standard deviation of 4.01.

We analyse the evolution along time with an  SPC chart:


It shows some out of control situations.

 Let us now measure autocorrelation of this data with Excel Data Analysis:


Each value is correlated with the previous one with a correlation index of 44%, this means there is a strong autocorrelation. This confirms the inertia effect due to the mass of the airplane.  

Let us compare this with a purely random process with a normal distribution:

In this case there is no evidence of autocorrelation: each outcome is independent of the previous ones.

Response delay

When you try to control this process the first thing you notice is that there is a delay between your adjustments and the tilt response:


This is the result of inertia: the response is slow.


Continuous Process Balancing by Fluid Accumulation in a Tank


Let us analize another example:

By accumulating a fluid in a tank we achieve a balancing effect which is useful to reduce the standard deviation of a critical metric.

Pure water has a pH of 7. 

Some local regulations require that water pH should be between 5.5 and 9.5 before it can be drained into a river.

In the following example accumulation in a tank has been used in order to reduce the pH standard deviation and meet the required regulations. 

The sewage water from the factory has an average pH of 5.68 with a standard deviation of 2.09. 

According to the previous regulations (specs) the resulting Cpk is 0.086 which is clearly unacceptable: we will often contravene the regulations.

This is an histogram of the pH of the factory sewage:


Tank Acumulation Effect 

After the sewage was accumulated in a pond we compare the pH of the input into the pond with the pH of the output drainned into the river: 


We can see variation has been significantly reduced.

The pH histogram of the output is now:


Resulting in an average pH of 5.99 and a standard deviation of 0.42 which gives a Cpk of 1.17 (a significant improvement from 0.08)

Let us now compare autocorrelation of input to the pond with output:



We can see a significant autocorrelation in the output produced by the pond accumulation. This had a positive effect in reducing the standard deviation of the pH to meet the regulations.


How to Manage Autocorrelation

If we want to control a process variable with an individuals control chart we have to meet two prerequisites:
  • It should follow a normal distribution
  • Each output should be independent of the previous ones: no autocorrelation


In the following example we have been measuring a critical process variable: Diwater resistivity with the following results shown in an SPC individuals chart:

Download this Excel file Resistivity.xlsx from OneDrive 

We notice continuous out of control situations which are mostly false alarms.

Checking for autocorrelation we obtain:


There is significant autocorrelation.

Exponential Smoothing with Excel Solver

If we want to use SPC to control this process, which has significant autocorrelation, we  can apply exponential smoothing EWMA to the data:


To do this we will calculate the transformed EWMA of RESISTIVITY:

EWMA(n) = LAMBDA * RESISTIVITY (n-1) + (1-LAMBDA) * EWMA(n-1)

Where LAMBDA is a number between 0 and 1

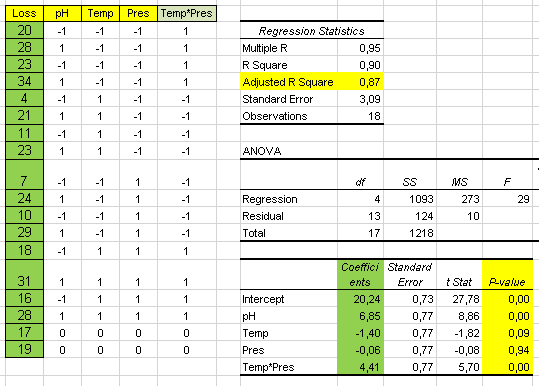
We will use Excel Solver to calculate LAMBDA to minimise the residuals in column C:

Residuals(n) = Resistivity(n) - EWMA(n)

We compute the total quadratic error (sum of squares) in 

E2 = SUMPRODUCT(C:C;C:C)

Now we ask Solver to minimise the total error in E2 by calculating LAMBDA in D2 with the restrictions that it should be between 0 and 1.

We obtain the result of LAMBDA = 0.284 

to obtain the minimum total error in E2 of 0.124

Now let's see the original Resistivity and transformed EWMA in a graph:

We are now going to use the resulting residuals in an SPC chart to control the process instead of the original Resistivity data:

We have now removed the false alarms from the SPC chart and keep only the real out-of-control symptoms.

Now let's check for Residuals autocorrelation:


We see no significant autocorrelation.

So this enables us to use an Individuals SPC chart with the residuals to detect Out-of-control situations of the original data without the false alarms. 

Conclusions

  • Process inertia shows with autocorrelation: metric values are dependent of previous values
  • Inertia causes a delay between action and response, which may produce over-reaction when you try to control the process
  • Mechanical inertia is proportional to the mass of the object (airplane, ship).
  • Fluid inertia is proportional to the volume of its storage in a tank or pond.
  • A flywheel is used in a car engine to smooth rotation speed, by increasing mechanical inertia.
  • Fluid accumulation in a tank is used to reduce variation.
  • Body weight has autocorrelation.
  • Autocorrelation could have a positive effect: it reduces standard deviation.
  • To control an autocorrelated variable, it may be transformed by exponential smoothing, then we control the residuals instead of the original variable.
  • All this can be done with Excel Data Analysis and Solver.



Comments

Post a Comment

Popular posts from this blog

Design of Experiments (DOE) with Excel

Image
Design of Experiments (DOE) is a very useful process improvement methodology.  Microsoft Excel has some powerful data analysis tools, which I have, successfully, used for DOE. When it comes to analyzing cause and effect, we want to know what process factors affect our outputs.   Correlation and Regression could give us an indication of the main factors, and the extent they affect the outputs. In some cases, there may be interactions among the different factors, or the mathematical relation between factors and outputs may not be linear. In these cases, it is useful to run a systematic set of experiments, to test all possible combinations of factors, to relate them to the outputs. Factorial Experiment Example We want to minimize process loss, and after some brainstorming among the process specialists, we concluded that 5 factors may affect loss. Based on current factor levels, we have selected the following levels to experiment with:    Download this Excel file DOE_w...
Read more

Response Surface Design Of Experiments with Excel

Image
Design of Experiments is a useful methodology for process improvement. The purpose is to find a relationship between process variables we can control and key process outputs in order to increase process capability . You can use Excel statistical analysis tools, Solver, Pivot charts, etc. to plan and analyse the results of these experiments. The first approach is to look for a linear relationship as shown in:   Excel DOE But in some cases this relationship may not be linear, in which case we will try a quadratic model with Response Surface DOE . We will use an example in this Excel file you can download: Download file   ExcelResponseSurface.xlsm   from OneDrive to your PC. In this example we are trying to maximize process yield acting on the critical factors pH , Temperature and Time . We will run the experiments in the Experiments simulation sheet using coded values.   Code pH Temperature Time -1 2 120 7 1 12 150 15 Factorial Experiments We start by ru...
Read more

Virtual Obeya Room

Image
The Obeya room is a "war room" used by process improvement teams to meet and solve critical multi functional problems.  The room walls are lined up with boards, highly visual charts and graphs showing program timing, milestones and progress to date and countermeasures to existing timing or technical problems.  The team meets in this room regularly but team members can also visit the room, which is fully dedicated to the project, throughout the day. What is an Obeya? Obeya Room Benefits Remove organizational barriers Visual management by displaying all relevant data required in the improvement project Encourage a collaborative environment through regular meetings Implement quicker, more effective solutions The whole team knows what is going on in real time Some Practical Constraints in the Implementation Some companies can't afford the luxury of a fully dedicated room Some of the team members may be located far away so they will only attend the meetings The data displayed ...
Read more