Random Variation Vs Trends



Understanding variation is key to interpret the value stream behavior. Not all variation is the same.


Variation



These are some factors which may add variation to the process of cooking a turkey. 

Every process has variation. Some causes of variation may be identified and acted upon.
We can use two metrics for variation which complement each other:




Manual Dice Throwing

This simple exercise can help to experience process variation and understand the difference between a process change and inherent process variation.
This understanding is key on management decisions to avoid both overreaction and lack of reaction.
To run the exercise with actual dice print the form:

Exercise:

  1. You will need a printed form and 4 dice for each team
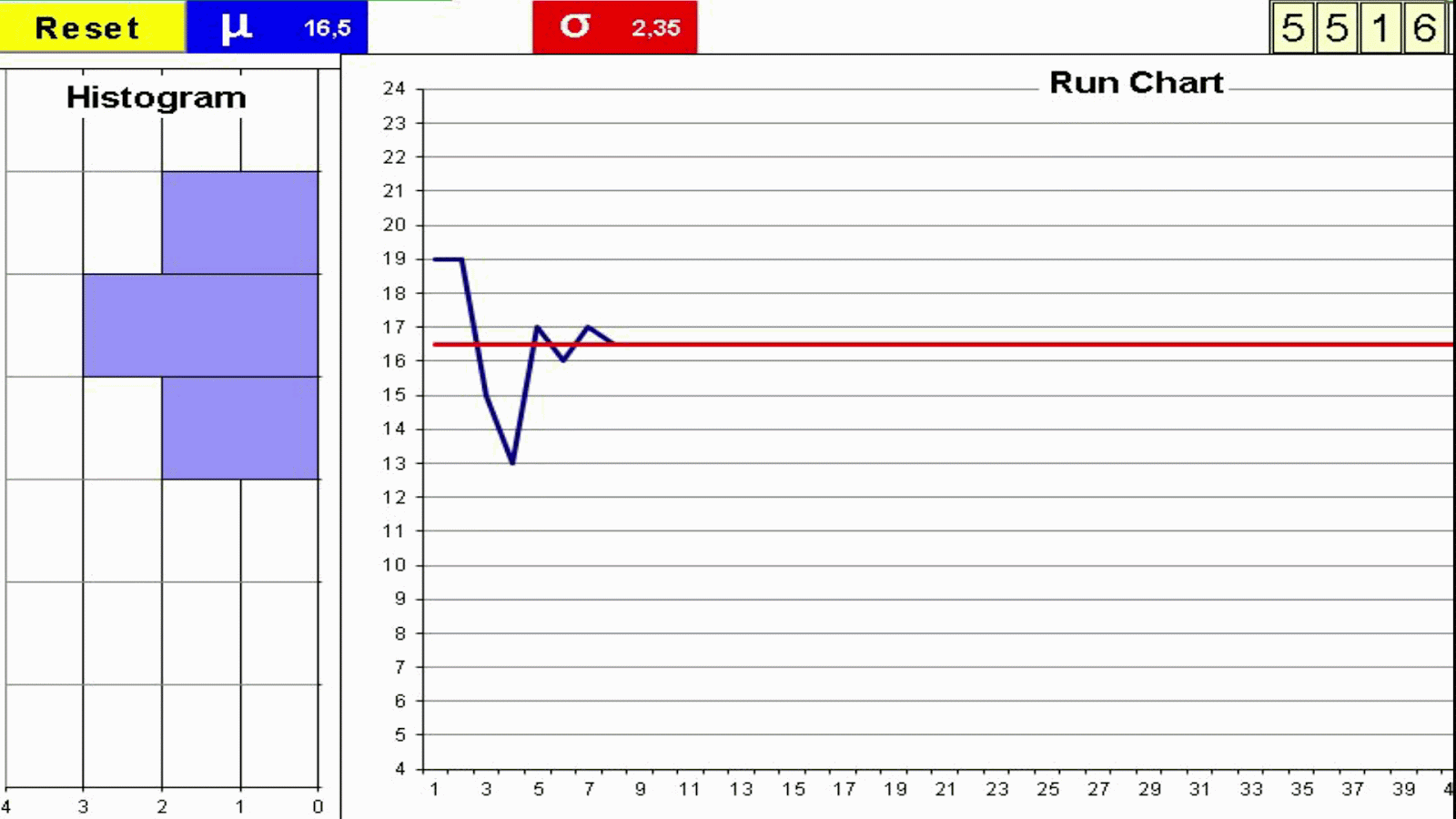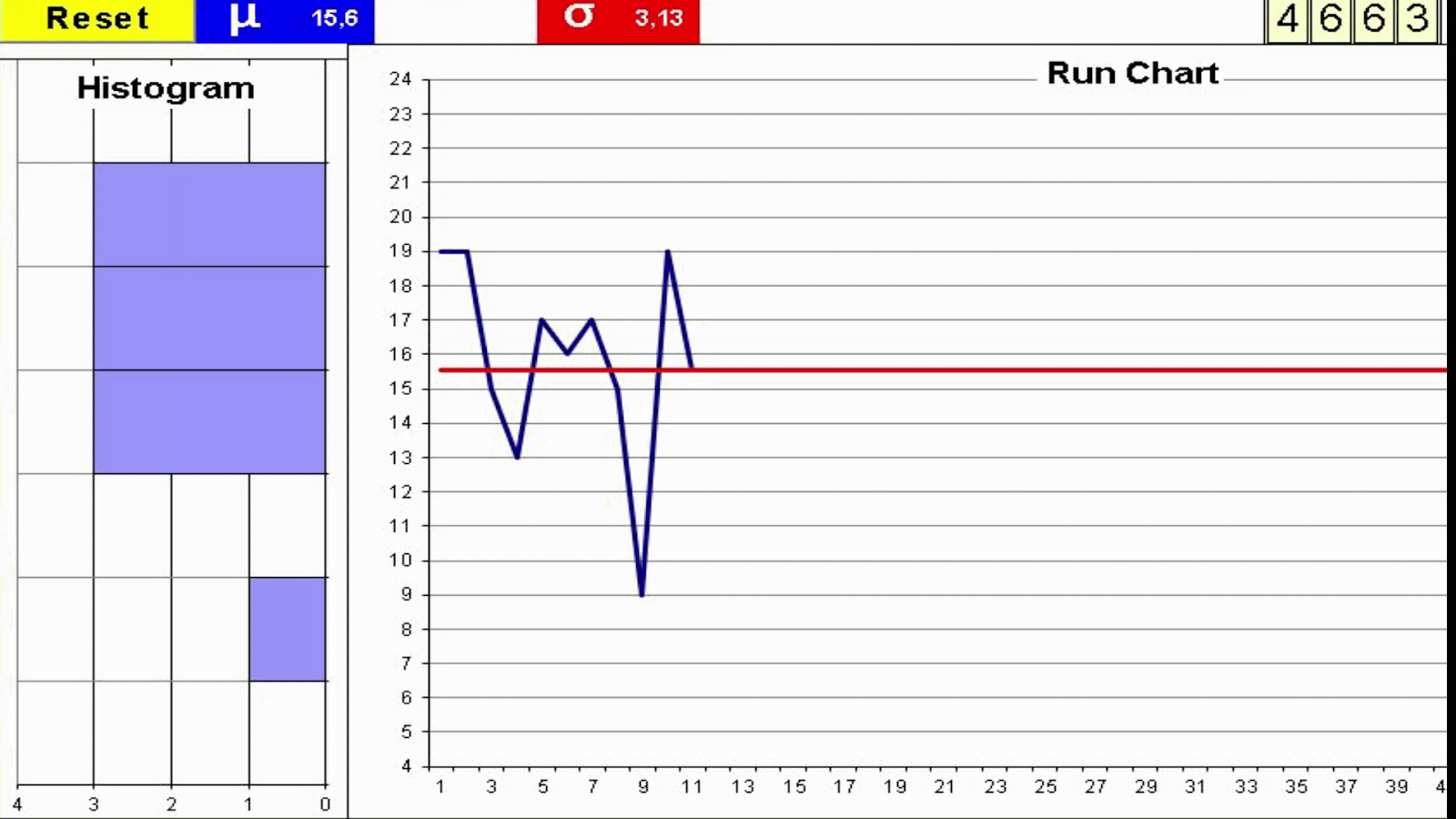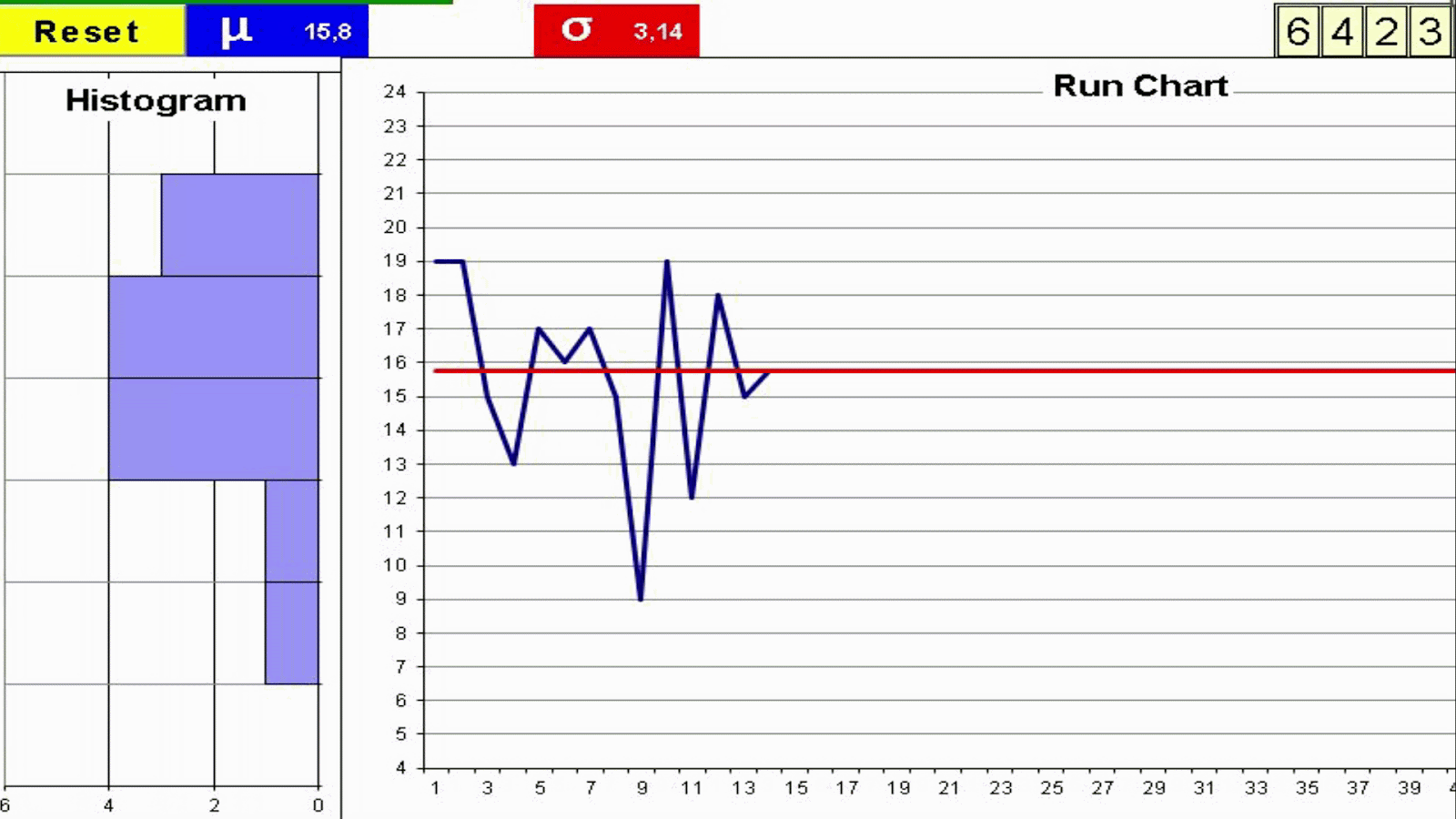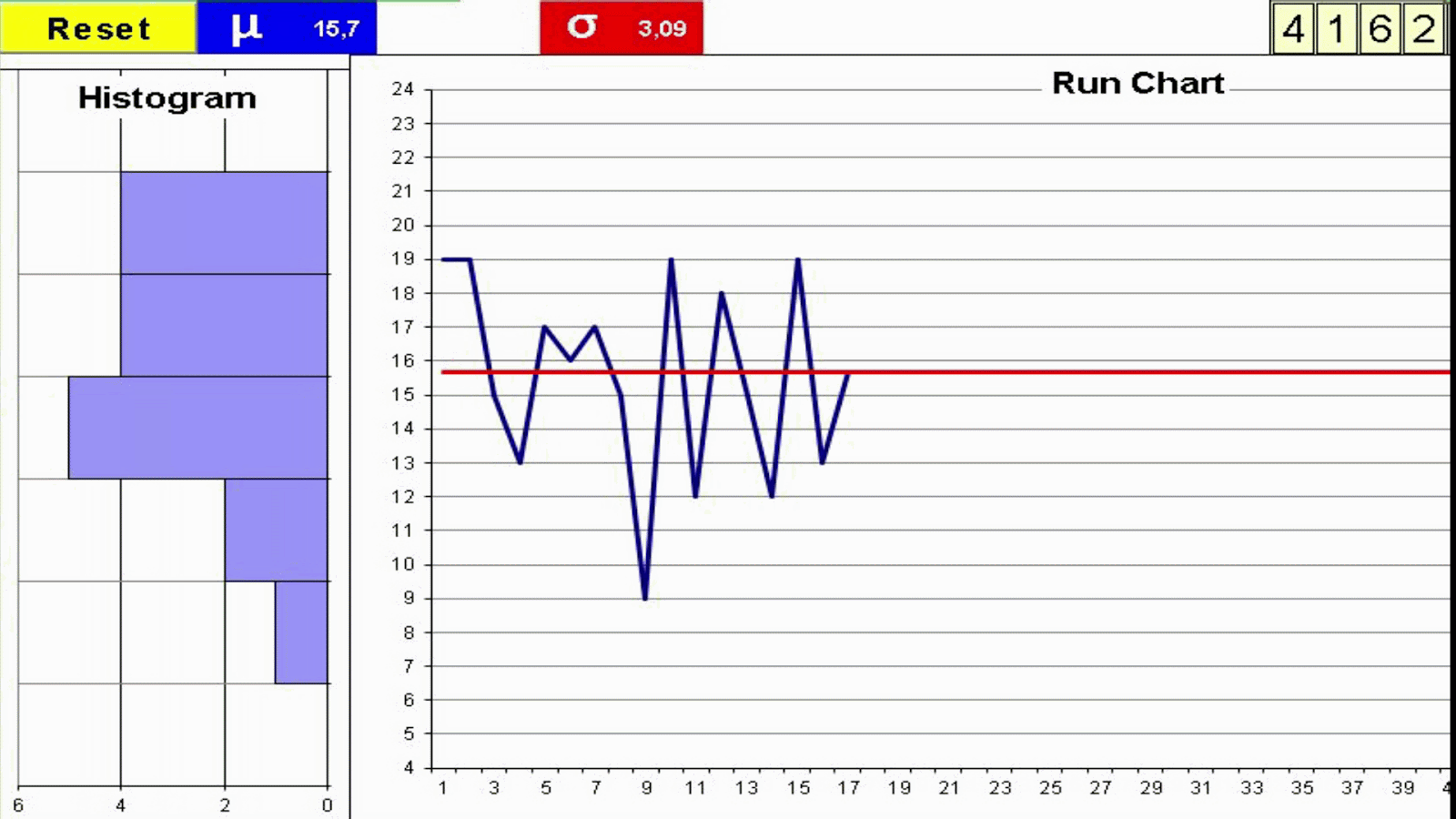
  2. Throw 4 dice and add the outcomes
  3. Record the result in the Run Chart
  4. Repeat 50 times
  5. Join the dots in the Run Chart with a line
  6. Build the Histogram by counting the total number of dots on each group of 3 values


Run this Exercise with a Simulator

Download this Excel file Variation.xlsm to your PC from OneDrive
Close all Excel sheets before you open this one and enable MACROS.



Press RESET in the DICE sheet and keep on pressing F9 to throw the 4 dice.


Results Interpretation Questions:

Try to answer these questions on each team and then discuss all teams together:
  1. Does each outcome depend on the previous one?
  2. Are there any special trends or indication of process change in the run chart? Is this a stable process?
  3. Is there a special cause that explains the maximum and the minimum values? Did you do anything different to obtain them?
  4. If we have a target to achieve the maximum possible value will motivation from management help?
  5. Is the frequency distribution close to normal: maximum at the center, declining frequency on both sides, symmetrical?
  6. What distribution would result throwing one single die? Why?
  7. Is it possible to predict the outcome of one specific throw?
  8. Is it possible to predict the frequency of one specific outcome for a large number of throws?
  9. Can two different run charts produce the same histogram

Answers:

1. Each outcome is independent of the previous one. This defies some widely accepted fallacies among gamblers:
2. We can't see any significant  trends up or down, therefore this is a stable process: it continues to behave the same way. It is stable in spite of its large variation. 
This is what we would expect since we have not changed the way we throw the dice so the process will continue to behave this way while we do so.

3. We did nothing different to obtain the high or the low values: the outcomes are purely random

4. Motivation will only produce frustration of the employee and no improvement in this case. The outcome in this case is purely random and the employee running this process has no way to improve it.
Some managers, in a case like this, may get the impression that the variation is a consequence of their own positive or negative employee motivation actions, but we know, in this case, it has nothing to do with it.

5. Yes, the histogram is close to normal: 


This is a stable process following a normal distribution with average 14 and standard deviation around 3.
Throwing 4 dice there is only one combination that gives a sum of 4 (all 1's) but there are many combinations that give a sum of 14. The distribution of sums of 4 throws follows a normal distribution in spite of the distribution of single values following a uniform distribution (Central limit theorem)

6. One die distribution: Uniform (all outcomes have the same probability)



7. It is not possible to predict any one outcome.

8. Yes, in this case of a stable process we can know the frequency of each outcome with the histogram above for a large number of throws.

9. Yes, two different run charts can produce the same histogram. The histogram can not tell us if the process is stable. This can be done with the run chart.

Stability doesn't necessarily mean that the process is OK: it just means that the process is neither improving nor getting worse.

 

Alternative process

Let's now analyse another process: Open Variation.xlsm sheet ALT, press RESET and keep pressing F9 to run the process.



Now try to answer these questions on each team and then discuss all teams together:
  1. Is this a stable process? Why?
  2. Is it likely that this data comes from the previous process of throwing 4 dice? Why?
  3. Can we use the frequency distribution histogram to predict process behavior in this case?
  4. What is the probability that values 7 - 13 happen again? Can you conclude that by looking at the histogram?
  5. What is the meaning of the frequency distribution histogram in this case?


Alternative Process Conclusions


1. We can clearly notice that this process has a significant upward trend, therefore it isn't a stable process: its average is shifting up.

2. Therefore it is very unlikely that it comes from throwing dice (apart from the values above 24 impossible with 4 dice).  

3. In this case of an unstable process, as shown by the Run Chart, the Histogram is completely misleading if we want to predict the process behavior.

4. The histogram predicts that values below 15 have a certain probability of occurring but from the Run Chart we see that this is very unlikely.

5. If the process is not stable, as shown by the run chart, the histogram is useless to predict future behavior.

We can conclude that the Run Chart and the Histogram are both necessary and they complement each other.

First we must check that the process is stable with the Run Chart and only if it is we can use the Histogram to characterize the process behavior.

Statistical Process Control (SPC)

The question is how do we know if the process is stable (apart from just our impression)? What is a significant trend? The answer is to use an SPC chart (sheet Alt SPC):


The green and red dots indicate a significant upward trend, therefore this is not a stable process. 
If it isn't stable we can't forecast how the process will behave in the future and our histogram is obviously useless.



Defect Rate Comparisons

Open Variation.xlsm sheet Defects


These are the defect rates produced by 6 operators during one week.

If you were the department manager you should decide, based on this data, whether to take some actions such as:
  1. Talk to Amparo to remind her of our zero defects commitment with the customer
  2. Congratulate Fernando for his results and, maybe, give him a prize
  3. Ask the process engineer to explain why Mondays produce more defects than Fridays
  4. Tell operators that anyone producing above 8% weekly average defects will be penalized


Corrective Actions Analysis

If you have decided on any of those actions you are wrong. In fact, they may be counter productive.
This would be an example of overreaction on the part of management due to a lack of understanding of process variation.
To see this just press F9 to simulate another week with this same process: your opinion on who is best or worst may change.
If we analyse the results of 4 weeks we notice that the differences among operators aren't that large

 



How do we know if there is a statistically significant difference among the different operators or days of the week?
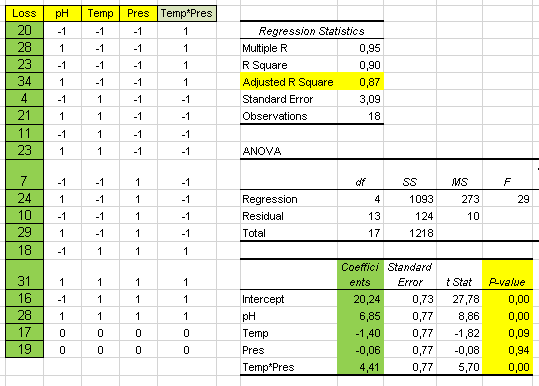
This analysis can be done with Data Analysis in Excel: 2 Factor Anova


Rows are the operators. The analysis of variance of the operators give us a p-value of 0.60 which is higher than 0.05 this means that there is no significant difference among the results of the different operators.
Columns are the days of the week. In this case p-value of 0.11 is also above 0.05 so, there are no significant differences among the days of the week.
Management improvement actions, in this case, should be directed to improve the overall process to reduce the defect rate. The process owner may run a Design Of Experiments (DOE) to optimize the critical process parameters to achieve this.

Process Control

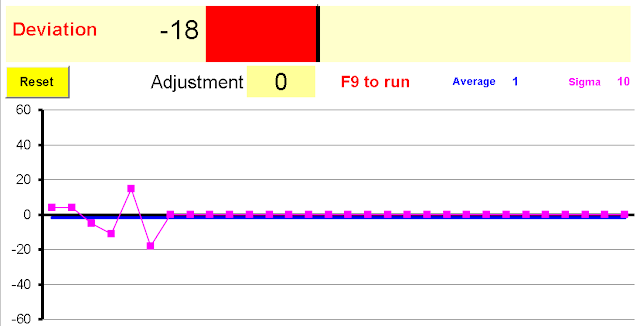
Open Variation.xlsm sheet Control and press Reset
  1. You have been made responsible to control a machine to insure the deviation from target is zero in every run
  2. You can set the adjustment value (positive or negative) to be applied to the next run
  3. Set the adjustment and press F9 for the next run
  4. Repeat for 25 runs



Analysis of Results

  1. Did you achieve your objectives of controlling the process to obtain zero deviation in every run?
  2. Why?
  3. What strategy did you follow?
  4. What could you have done differently?
  5. Can you be held responsible for these results?
  6. Why?
These are the results of overreaction by making Adjustment = - Deviation:


If we made no adjustments at all:


The average with or without adjustments is close to zero but the standard deviation with adjustments (38) is much higher than with no adjustments (14). This means that with all our efforts we have made the process worse.

Before we start making adjustments we should have seen how the process behaves with no adjustments:


 We see that the process has random variation and its average deviation is well centered in zero: this means we can't improve it with our adjustments, in fact, we will increase the variation and make it worse.
 In this case the operator has been given an impossible task.

Adjusting the site after every shot:  Over-reaction


Conclusions

Comments

Post a Comment

Popular posts from this blog

Design of Experiments (DOE) with Excel

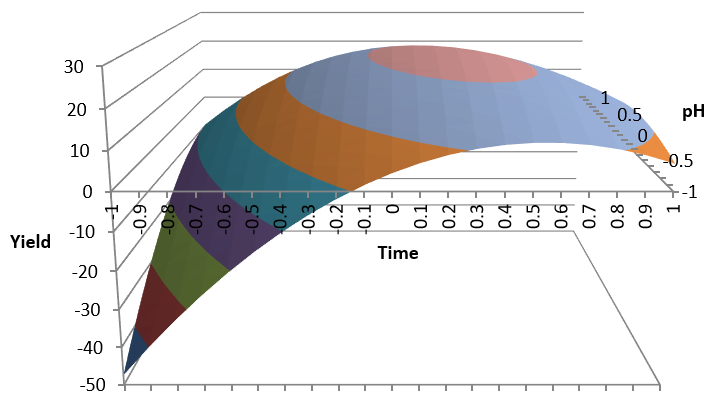
Image
Design of Experiments (DOE) is a very useful process improvement methodology.  Microsoft Excel has some powerful data analysis tools, which I have, successfully, used for DOE. When it comes to analyzing cause and effect, we want to know what process factors affect our outputs.   Correlation and Regression could give us an indication of the main factors, and the extent they affect the outputs. In some cases, there may be interactions among the different factors, or the mathematical relation between factors and outputs may not be linear. In these cases, it is useful to run a systematic set of experiments, to test all possible combinations of factors, to relate them to the outputs. Factorial Experiment Example We want to minimize process loss, and after some brainstorming among the process specialists, we concluded that 5 factors may affect loss. Based on current factor levels, we have selected the following levels to experiment with:    Download this Excel file DOE_with_Excel.xlsm fro
Read more

Response Surface Design Of Experiments with Excel

Image
Design of Experiments is a useful methodology for process improvement. The purpose is to find a relationship between process variables we can control and key process outputs in order to increase process capability . You can use Excel statistical analysis tools, Solver, Pivot charts, etc. to plan and analyse the results of these experiments. The first approach is to look for a linear relationship as shown in:   Excel DOE But in some cases this relationship may not be linear, in which case we will try a quadratic model with Response Surface DOE . We will use an example in this Excel file you can download: Download file   ExcelResponseSurface.xlsm   from OneDrive to your PC. In this example we are trying to maximize process yield acting on the critical factors pH , Temperature and Time . We will run the experiments in the Experiments simulation sheet using coded values.   Code pH Temperature Time -1 2 120 7 1 12 150 15 Factorial Experiments We start by running a full factorial experi
Read more

Six Sigma Virtual Catapult with Excel

Image
  A wooden catapult has been widely used in Six Sigma education to illustrate multiple factor process variation and optimization. We will use a catapult simulator with 4 factors to practice: Process variation Linear regression Response surface analysis Process optimization This will be done using Microsoft Excel Analysis and Solver Download this Excel simulator Catapult.xlsx from One Drive Working Plan 1. What factors affect distance? 2. What values of these factors to achieve maximum distance? 3. Run a full factorial set of experiments with 4 central points 4. Can you detect curvature? Is this linear model valid? 5. Run response surface experiments to find a better model 6. What is the resulting formula to estimate distance as a function of factors? 7. What values give us the maximum distance? 8. Make 10 replicates to estimate the confidence iterval of the distance 9. Calculate the angle a to hit a target of 20 with maximum or minimum values of f, m and l Possible Facto
Read more