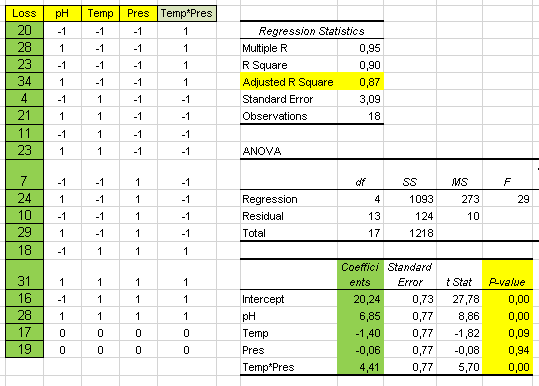
Statistical Process Control with Excel
Statistical Process Control (SPC) is used to control a critical process output, acting on the factors affecting it, only when required.
The purpose is to differentiate between a statistically significant change in the process, and common cause variation, because the actions required will be different.
Process stability is a prerequisite for any further analysis. If a process is not stable, any conclusions you draw, can't be assumed to hold in the future. With SPC we check for process stability in the future.
Control over-reaction
A case of over-reaction is illustrated by the following example:
The correct way is, of course, to fire 5 or 6 shots without adjustments, and then decide if adjustment is required, based on the center of the impacts.
Control under-reaction
This is an example of under-reaction:
Many companies have fallen into this trap:
A big disaster generates a quick and effective response, and the company recovers
On the other hand, a slow degradation of their KPIs, such as customer sat, or delays, pass undetected until it is too late.
SPC Chart Interpretation
SPC uses some rules, developed by the Western Electric company, to detect symptoms of statistically significant variation.
These are some of these symptoms of lack of stability:
Trend symptoms
2 out of 3 consecutive values in zone A indicates a trend.
4 out of 5 consecutive values in zone B, is an indication of trend.
Statistical Process Control Chart:
In our charts, red dots indicate upward trend symptoms, and green dots downward.These are some upward symptoms definitions:
Daily Weight Control SPC Example
SPC Charts for Variables and Attributes
We will now analyze some of the charts used for variables and attributes.
Download this Excel file SPC.xlsx from One Drive with the examples we will use
Individuals SPC chart
In sheet Change we have collected process yield data every hour, during several shifts.
Since we collect a single value each hour, we are using a variables SPC chart for individuals. This chart can be complemented with a moving range chart, where the absolute value of differences between each value and the one preceding is plotted.
We automatically apply the Western Electric rules for Out-Of-Control symptoms and the alert description will appear in the corresponding row: 15 - 24When any of these alerts appear the corresponding point in the chart will be coloured: In red: upward symptom. In green: downward symptom
While there are no color dots the process is stable: there are no statistically significant changes.
Process Change
Looking at the chart above, we see green dots from 10:00 to 16:00 on 10/04, and red dots between 1:00 and 3:00 on 11/04 during the night. We can notice a jump from 16:00 to 17:00 which might indicate the moment when the process has changed, but this jump is not significant enough to declare it as a process change.It is not until 1:00 that we have enough evidence to declare that the process has changed.
In this case, since we are measuring yield, an increase in yield is an improvement.
So, we can say that process yield has improved sometime between 16:00 and 1:00. With this information we should now investigate what happened during this period that caused this improvement.
How much have we improved? If we compute the average between 6:00 and 16:00 we get an average yield of 93. And from 17:00 to 11:00 the next day 118. So, we can estimate an average yield increase of 25.
Process Change Alerts
Looking at the alert details in the bottom rows we see that from 10:00 to 16:00 we have 4 out of 5 consecutive values 1 sigma below the center line: values significantly below the average. The value -9 at 14:00 means that the last 9 values were below the center line: same interpretation.
The values 9 starting at 1:00 on 11/04 mean that from 17:00 to 3:00 all values have been above the center line: yield has significantly increased.
Normality Test
We see the histogram which doesn't seem to have a bell shape but the p value 0.351 for the test of normality well above alpha of 0.05 confirms that there is no evidence of lack of normality.
X bar s Chart
This is a common SPC chart for variables (see Xbar S sheet)Instead of making one single measurement we make several: in this case 4.In this example we have taken 4 measurements of a critical dimension every hour.
Each hour we compute the average and the standard deviation of these 4 measurements.
We use 2 charts: in one we plot the averages and in the other the standard deviation.
We apply the same Western Electric rules to each of the charts. Any out-of-control symptoms in one of the charts will indicate a significant process change.
In the case of the standard deviation chart the interpretation is different: red is bad (variation increase) and green is good (variation decrease).
Operators must be trained to interpret these out-of-control situations, to make the required corrections in the process as soon a possible.
Slow Trend
Let's interpret the chart in sheet Slow Trend:
Looking at the chart we can graphically detect an upward trend which in this case of yield is a good thing: our process is improving significantly from the statistical point of view.
This trend is confirmed by the green dots up to 6:00 in day 11 followed by red dots starting at 12:00 until the end.
The interpretation of this situation is that we have a continuous process improvement starting around 11:00 on day 11, maybe due to some ongoing improvement actions.
The alerts of the chart:
- One value at 7:00 below the lower control limit
- Six values from 10/4 14:00 to 11/4 1:00 where 4 out of 5 consecutive values 1 sigma below the center line
- Five values from 10/4 8:00 to 11/4 6:00 where 2 out of 3 consecutive values 2 sigma below the center
- Four values, starting from 11/4 11:00 above the upper control limit
- Eight values, from 11/4 11:00, where 2 out of 3 consecutive values 2 sigma above the center
- Eight values, from 11/4 14:00, where 4 out of 5 consecutive values are 1 sigma above the center
- Three values, from 11/4 19:00, where 9 consecutive values are above the center
Day of the Week Effect
We now analyze sheet DOW:
Here we are collecting daily production data, and we notice that our average production is 400, and our Individuals SPC chart is not detecting any significant changes in the process.
On the other hand, we can see a repetitive cycle of 7 days, which of course, corresponds to a week.
If we look in our calendar, the days of lowest production, we realize they correspond to Sundays, and the next lowest to Saturdays.
This is telling us that maybe, there is a significant seasonal trend within each week.
In order to check that, we have added column DOW to our spreadsheet DOW2, where we calculate the day of the week, corresponding to each date with this formula:
Where A2 holds the date and "2" is to start counting the week on Monday.
The confidence intervals for the average production each day of the week (1 = Monday) is:
On the other hand, we can see a repetitive cycle of 7 days, which of course, corresponds to a week.
If we look in our calendar, the days of lowest production, we realize they correspond to Sundays, and the next lowest to Saturdays.
This is telling us that maybe, there is a significant seasonal trend within each week.
In order to check that, we have added column DOW to our spreadsheet DOW2, where we calculate the day of the week, corresponding to each date with this formula:
Where A2 holds the date and "2" is to start counting the week on Monday.
The confidence intervals for the average production each day of the week (1 = Monday) is:
We can now confirm that there are significant differences, among the different days of the week:
- Wednesdays (3) and Fridays (5), have the highest productions.
- On Thursdays (4), for some reason, it is significantly lower and, of course
- it is lowest on Saturdays (6) and Sundays (7).
Process Time
We have been collecting daily process time during 3 months in sheet Time and we want to know if there are any significant changes in process time during these 3 months.Since we have a single value each day we will use a variables SPC chart for individuals.
We need our values to follow a normal distribution in order to use this chart so we will do a test for normality in BasicStats Time:
This is what we would expect: time measurement typically follows a skewed distribution for a simple reason:
- There is always a physical lower limit in time
- On the other hand, there is no upper limit: time may be extended by all sorts of defects or difficulties,
In this case we can look for a data transformation that will make the data follow a normal distribution.
Box-Cox Data Transformation
This is a data transformation of the sort y = x ^ λ where we calculate the value of λ to produce a normal distribution. We will calculate this value from the Time data in column A of sheet Box Cox:
To calculate λ we will use Excel Solver:
- Calculate lambda in cell I8 by maximizing cell I6
- The restrictions are -5 <= λ <= 5
- The resulting value is λ = - 0.348
- In column F we obtain the transformed data.
We will now check if this transformed data follows indeed a normal distribution in sheet BasicStats Transformed:
Checking the normality of this transformed data we obtain a p value 0.717 which confirms that this data is now normal ( p > 0.05).
Now we can use an Individuals Variables SPC chart with this transformed data in sheet SPC Transf:
So we are controlling with SPC the transformed data instead of the original data and we see no out of control symptoms in this case: our Process Time is stable in spite of its high variance.
This means it has not changed significantly along these three months.
Attribute SPC Chart P for Proportion of Defectives (Sheet P)
When we have a Go / No go check in our process the data collected follows a Binomial distribution: there are only 2 possible values.
Then we can use a P chart to control the proportion of defective units:
- Sample size (Number of units controlled during the day)
- Number of defective units found
We can't just collect the proportions p because we need the sample size for the SPC calculations.
If you look at the upper control limit in red you notice that it is not a straight line in this case, the reason is that sample sizes are varying and this affects the control limit: the larger the sample size the lower the limit.
The average proportion of defectives is shown by the center line in blue which in this case is 0.01 (1% defectives).
The same Western Electric out-of-control symptoms apply to this p chart as before.
Attribute SPC Chart U for Defects Per Unit (DPU)
We must distinguish between Defectives and Defects.
On the other hand one unit may have more than one defect so the distribution of defects follows a Poisson distribution.
The aspect of a Poisson distribution may look like a variables distribution but it is very different: the Poisson distribution only has integer numbers in the x axis: an individual unit may have 2 defects or 3 but it couldn't have 2.8 defects.
DPU can be any real number greater or equal than zero.
Sheet U has an example of a U chart:
This information can be useful to understand the reason for these process improvements: time stamps will let as associate changes we made in the line with the improvements.
In sheet Dist Defects we have used a Pivot Graph to plot the distribution of defects in the samples of 10:
Average defects per sample of 10 is 4 so average DPU = 0.4
Conclusions
- Real Time SPC is a useful tool for operators to control their process, by making the required adjustments, as soon as needed, but without over-reacting.
- Control charts are useless, unless analysis and corrective actions are done in real time.
- To do this, data must be collected on the spot and charts updated fast enough.
- Operators need to be trained, to know what corrective action is required on each case.
- Variables SPC charts of critical process parameters, are more accurate than attributes, and they enable process adjustments before defects start to appear.
- Variables charts for individuals, require normality, so you may need data transformation.
- Being in control is not enough. We must make sure the process meets the customer requirements. After we insure that the process is stable, Process capability measures to what extent is the process able to satisfy the customer.
Comments
Post a Comment