Process Control and Capability

 



The first step for process improvement is stability. We analyse this with Statistical Process Control.

As a result of this analysis we may find out-of-control situations due to special causes. We need to resolve these causes to make the process stable. 

Stability means the process is behaving in a predictable way but it doesn't necessarily mean it meets the customer expectations. 

To find out to what extent is the process able to meet the customer expectations we measure Process Capability.


Descriptive Statistics with Excel

Download a copy of Excel file  Capability.xlsx  from OneDrive on to your PC to run it.
In sheet Diameter we have placed in column A our data consisting of 500 measurements of a critical diameter.

After being confident that our process is stable we can characterize it with descriptive statistics in Excel Data Analysis:


 

These are the results: basic statistics of our data


 Frequency Distribution Histogram

The histogram gives a graphical representation of the variable we are dealing with in our process:


Result:

We see a bell shaped distribution typical of a normal (Gaussian) distribution. We see that it is quite symmetrical  and its mean, median and mode are very similar. This is a very common distribution in nature and many process metrics. 

Let us now analyse another metric which typically follows a quite different distribution.

Process Lead Time

In sheet Lead time We have collected process lead time (hours).
We do the same analysis:



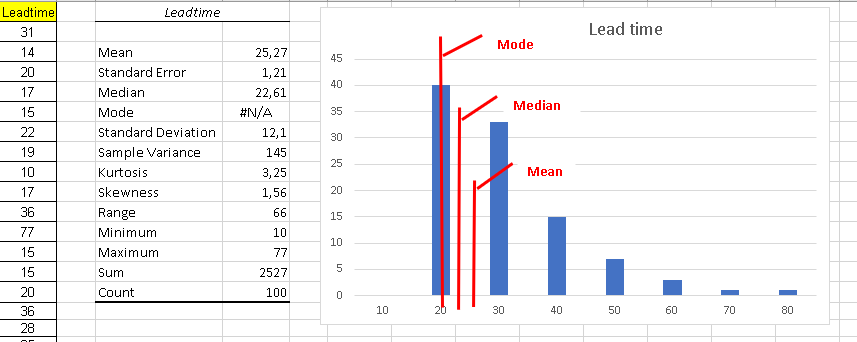
In this case we see a very skewed distribution 

We also notice that Mode, Mean and Median are quite different:

Test for Normality

We want to know to what extent is our diameter distribution normal (Gaussian). We do this normality test  in sheet BasicStats diameter:


We can confirm this diameter data follows a normal distribution (p value 0.466 > alpha 0.05)

Let us check now manufacturing lead time normality replacing the data in column B with that of Leadtime.



In this case the distribution is very skewed. So lack of normality is confirmed:  p = 0  <  0.05 

This is something common with time measurements. The reason for the skewness of time distributions is that:
  1.  there is always a physical limitation which makes it impossible for a time metric to be below a certain limit. In this example this limit may be around 8 hours. 
  2. there is no upper limit: things may go wrong and time can become very large.

Customer Requirements

All processes have a customer: either the final, external, customer or an internal customer. 
In our process metrics we need to know, not only the nominal value required by the customer but also the spec limits. 

For a mathematician the nominal value may be enough, but in real life we know it is impossible to meet any real value: there is always an error (even if it is just a few microns). 

The spec limits indicate where the customer starts having real problems when using our product. 


Customer specifications are still necessary in the times of Six Sigma but their interpretation has changed:


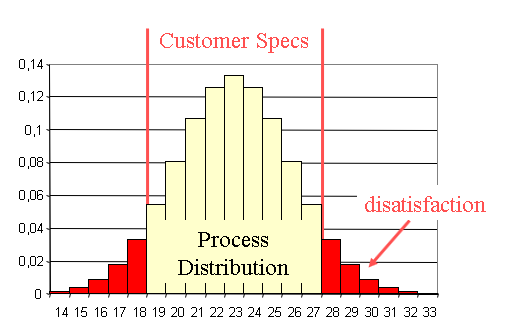
In football as long as the ball enters the goal it counts. In the new approach being within specs is not enough: you better keep away from the limits or else you have a chance of falling over.

Today meeting the customer specifications is not enough: we must prove to our customer that our process is very unlikely to produce a single part outside the specs. 

We use the process capability metrics to measure to what extent is our process able to systematically satisfy the customer (meet the customer specs).

Imagine you measure a critical dimension of the parts you just received from your supplier and they are all within your the spec limit 



In the old times you would just accept these parts. But those parts close to the spec limit will probably cause you problems. Also:




Process Capability

  
Assuming our process is stable the histogram characterizes the process behavior. We need to compare this with the customer requirements represented by the specs.


Process Capability Index Cp

The process capability index Cp is the rate between the spec range specified by the customer and our process variation measured by six times the standard deviation:

Cp = (USL -LSL) / (6 σ)



Process Capability Index Cpk

Index Cp is not enough to warrant meeting the specs. If the average of our distribution is not in the center of the spec range we may be out of spec in spite of our narrow distribution. 

So we need another index which takes into account the centering of the distribution: Cpk 


When the distribution is centered in the spec range Cp = Cpk. If not Cpk < Cp. 

  • Centering the distribution can, sometimes, be achieved by an adjustment. This will improve Cpk making it closer to Cp. 
  • Improving Cp means reducing the standard deviation which is typically much more difficult.

Single-sided Specifications

In some cases we only have one spec limit:



Common Mistakes with Capability Indices


Diameter Example Capability

In the previous diameter example we concluded:
    • Mean = 99.81
    • Standard deviation = 9.77
    • Sample size = 500
    • Normal distribution (p = 0.466)
If the customer spec limits are:
    • USL = 110
    • LSL = 95
Before we calculate Cp and Cpk we need to ensure that the process is stable. We will use an Individuals Variables SPC Chart in sheet SPC ind:


We see no out-of-control symptoms so the process is stable. 

Now that we know the process is stable and follows a normal distribution we can go ahead and calculate Cp and Cpk:

Cp = (USL -LSL) / (6 σ) = (110 - 95) / (6 * 9.77) = 0.25

To calculate Cpk we look for the nearest spec limit to the mean: LSL = 95

Cpk = (Mean - LSL) / (3 σ) = (99.81 - 95) / (3 * 9.77) = 0.16

We notice that both Cp and Cpk are totally unacceptable.

A Six Sigma process is one with Cpk > 1.5  

In a case like this the first step must be to center the process in the spec range: 

Make the mean = (110 + 95)/ 2 = 102.5

And the next step would be to reduce the standard deviation (more difficult)

Lead time Capability

In our previous analysis we concluded:
    • Mean = 25.27
    • Standard deviation = 12.05
    • Sample size = 100
    • Distribution not normal
In this case we want lead time to be less than 50 hours so we only have an upper spec limit:
    • USL = 50 hours
The prerequisite of normality is not met so we can't calculate Cp and Cpk. 

The solution is to transform the data. We will try a Box-Cox transformation.

Box-Cox Data Transformation to Achieve Normality

We copy the data to the BoxCox sheet:



Now we use Solver to calculate the Lambda value in cell I8 to maximize cell I6. 

The resulting lambda value is -0.348 and in column F we already have the transformed data. 

We will now check that this transformed data follows a normal distribution by copying it to the BasicStats transformed sheet:


We have, indeed, achieved normality (p = 0.717 > 0.05)  

We now check for process stability with the transformed data in SPC transformed sheet:


The process is stable: no out-of-control alerts. 

To calculate Cp and Cpk we need to transform the USL of 50 hours.

We must notice that as time increases the transformed values decrease so the Upper Spec Limit will be transformed into a Lower Spec Limit:

Transformed LSL = 50 ^ (-0.348) = 0.256

We get the mean 0.34 of the transformed data from BasicStats transformed sheet:

When we have just one spec limit Cp makes no sense. 

We can just calculate Cpk:

Cpk = (0.34 - 0.256) / (3 * 0.05) = 0.56

To find out %  late:

=NORMDIST (0,256 ; 0,34 ; 0,05 ;1)  = 4.7 % late


Cpk and Ppk

In industry apart from these indices they use another two: Pp and Ppk.

In this case what we have been calculating using the standard deviation of all the data  (sigma overall) they call Pp and Ppk.

And what they call Cp and Cpk are calculated from an estimate of the standard deviation derived from the average range in an Xbar & R chart. 

This calculation requires making several measurements (typically 5) on each instance instead of just one measurement used so far.

The Xbar chart is made with means of each set of 5 values. The Range chart is made calculating the ranges of the 5 values (maximum - minimum). 

With this way of calculating these indices, only intrinsic variability is included in the sigma estimate so this gives a lower value for this sigma estimate and therefore higher values for the indices. 

This is an example to illustrate these calculations:

 
The sigma estimate 0.18 is lower than the overall sigma 0.23 so the computed Cp and Cpk are higher than Pp and Ppk.

Attribute Process Capability

So far we have been dealing with variables, but sometimes we only have attributes such as Pass/ Fail or Defects per Unit. 

Variables can be converted to attributes: for instance we can count the number of items out of spec.

Going back to the diameter example above we can compute the % of parts above the USL and below the LSL. 
    • Mean = 99.81
    • Standard deviation = 9.77
    • Normal distribution (p = 0.466)
    • USL = 110
    • LSL = 95
Since the distribution is normal we can compute the proportion of parts below the LSL:

= NORM.DIST (95 ; 99.81 ; 9.77 ; 1) = 0.31 = 31.1 % 

To calculate proportion above the USL:

= 1 - NORM.DIST (110 ; 99.81 ; 9.77 ; 1) = 14.8 % 

The total proportion of out-of-spec will be the sum of these two. The proportion of parts OK therefore:

Yield or % OK = (1 - 0.311 - 0.148) = 0.541 = 54.1 %




 In this histogram we can see the proportions of parts within the limits and out of spec. With attribute metrics of the type Pass/ Fail we have a binomial distribution and we can measure capability with yield (proportion of pass)


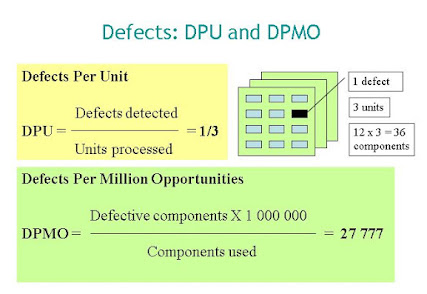
DPU and DPMO

Another attribute metric is number of defects. In this case we have a Poisson distribution and we can use two capability metrics: DPU and DPMO.
In this example of one defect in 3 boards DPU is 0.33 defects per board .
From the board assembly process point of view there is one defective component out 36 components used which is 27,777 defective components per million opportunities.

DPU (Defects per unit) is a metric from the customer perspective. 

DPMO (Defects per million opportunities) is a useful internal metric for process improvement:




Sigma Capability

A capability metric used for business processes  is Sigma Capability:

This metric is equivalent to Cpk when there is only one spec limit:

Sigma Capability = 1.5 + 3 Cpk

    • Six Sigma comes from Sigma Capability = 6  
    • which is equivalent to Cpk = 1.5  
    • or 3.4 ppm defective

Capability Metrics Conversion

You can use this conversion table in sheet Capability:

These conversions apply when there is only one relevant spec limit


Control Limits Vs Spec Limits

Control limits are derived from the data we have collected from our process. These are to be used by the operator to make sure the process continues to be stable.

Spec limits are imposed by the customer and the process owner must insure our process is capable to meet them.

These are some situations:







Conclusions

  • Process capability measures the ability of the process to meet the customer requirements
  • The customer may be the final customer or the next process using our output
  • Meeting the specifications is not enough. Capability insures they will also be met in the future
  • A capability study requires the process to be under statistical control
  • The process must follow a normal distribution for the capability indices to be valid
  • Data can usually be transformed to achieve normality
  • SPC is used by operators to keep the process in control
  • Process capability improvement is the process owner's responsibility 
  • Process Data Analysis can be used to improve capability
  • Design of Experiments may also be used 

Comments

Post a Comment

Popular posts from this blog

Design of Experiments (DOE) with Excel

Image
Design of Experiments (DOE) is a very useful process improvement methodology.  Microsoft Excel has some powerful data analysis tools, which I have, successfully, used for DOE. When it comes to analyzing cause and effect, we want to know what process factors affect our outputs.   Correlation and Regression could give us an indication of the main factors, and the extent they affect the outputs. In some cases, there may be interactions among the different factors, or the mathematical relation between factors and outputs may not be linear. In these cases, it is useful to run a systematic set of experiments, to test all possible combinations of factors, to relate them to the outputs. Factorial Experiment Example We want to minimize process loss, and after some brainstorming among the process specialists, we concluded that 5 factors may affect loss. Based on current factor levels, we have selected the following levels to experiment with:    Download this Excel file DOE_w...
Read more

Response Surface Design Of Experiments with Excel

Image
Design of Experiments is a useful methodology for process improvement. The purpose is to find a relationship between process variables we can control and key process outputs in order to increase process capability . You can use Excel statistical analysis tools, Solver, Pivot charts, etc. to plan and analyse the results of these experiments. The first approach is to look for a linear relationship as shown in:   Excel DOE But in some cases this relationship may not be linear, in which case we will try a quadratic model with Response Surface DOE . We will use an example in this Excel file you can download: Download file   ExcelResponseSurface.xlsm   from OneDrive to your PC. In this example we are trying to maximize process yield acting on the critical factors pH , Temperature and Time . We will run the experiments in the Experiments simulation sheet using coded values.   Code pH Temperature Time -1 2 120 7 1 12 150 15 Factorial Experiments We start by ru...
Read more

Virtual Obeya Room

Image
The Obeya room is a "war room" used by process improvement teams to meet and solve critical multi functional problems.  The room walls are lined up with boards, highly visual charts and graphs showing program timing, milestones and progress to date and countermeasures to existing timing or technical problems.  The team meets in this room regularly but team members can also visit the room, which is fully dedicated to the project, throughout the day. What is an Obeya? Obeya Room Benefits Remove organizational barriers Visual management by displaying all relevant data required in the improvement project Encourage a collaborative environment through regular meetings Implement quicker, more effective solutions The whole team knows what is going on in real time Some Practical Constraints in the Implementation Some companies can't afford the luxury of a fully dedicated room Some of the team members may be located far away so they will only attend the meetings The data displayed ...
Read more