Value Stream Data Analysis with Excel

- Map it as it is really happening today in Gemba with a Value Stream Map.
- Collect process data in the line.
- To understand the value stream dynamic behavior we will need statistically significant data to enable simulation
- Check for stability with Statistical Process Control
- Know to what extent it is able to meet the customer requirements with Process Capability
- Perform additional data analysis to get to the root cause
Hypothesis Testing
- Null hypothesis H0
- Alternative hypothesis Ha
Logical Sequence
- Start by assuming that H0 is true
- Try to prove Ha
- If you find enough evidence to prove Ha then you can reject H0
- If you don't find enough evidence you fail to reject it. This doesn't prove that H0 is true.
Example of a Comparative Statement
H0: "All trees are green"Truth Tables







Confidence intervals are another alternative to hypothesis testing
Download Excel file Data Analysis.xlsx from OneDrive to your PC to run the following examples.
Variables Confidence Intervals Analysis
In Sheet Variable we have an example of confidence interval comparisons:

- Sample size
- Sample mean
- Sample standard deviation
- Confidence level
- If we compare samples A and B: an increase of the mean just shifts up the interval
- Comparing A and C: an increase of the standard deviation increases the size of the interval
- Comparing A and D: an increase of the sample size decreases the size of the interval

- In this case we see intervals are not symmetrical as in the case of means
- Comparing A and B: Standard deviation in independent of the mean, therefore its interval is not affected
- Comparing A and C: Increasing the standard deviation its interval shifts up and increases in size
- Comparing A and D: the increase of sample size reduces the interval
Attributes Confidence Intervals Analysis

- If we compare A and B: Reducing fails shifts down the interval and reduces its size
- Comparing A and C: The average proportion is still 10% but the size of the interval is reduced
Variables and Attributes Tests
- We are going to analyse continuous and discrete data.
- For continuous data we will analyse the mean and the standard deviation
- For discrete data: proportions
- Versus the standard
- Two samples
- More than 2 samples

Test Conditions
1 Sample Test for the Mean
We are looking to increase our capacity and a supplier has suggested a piece of equipment to do that. The current average capacity of our equipment is 5000 units/ hour with a standard deviation of 500.
We have tested the new equipment taking a random sample of 20 hours of production obtaining an average production of 5150 units/ hour. Can we say that the capacity of the new equipment is higher than our current one? We accept a 5% error in our decision.
We can use the confidence interval as shown in sheet 1t:



2 Sample Test for the Mean



Multiple Means Analysis with Anova




2 Factor Anova
- Morning from 6:00 to 14:00
- Afternoon from 14:00 to 22:00
- Night from 22:00 to 6:00





Paired Comparison
We want to compare the durability of materials used for children shoe soles.
To do that we took a sample of 20 children and measured the duration of their shoe soles with one material and then the same children with the other material keeping track of what child had what results. The results are in sheet Shoes.
We start our analysis with a two sample t-Test:
Although the average duration of material B is 61 days Vs 54 days for material A the p value of 0.19 > 0.05 tells me this difference is not significant.
The reason may be the fact that there is a huge variation in duration depending on the child.
Since we have collected the data of which child had which duration we are able to do a paired comparison of this data:
This paired comparison eliminates the effect of the huge variation among the children and it confirms that the difference in duration between materials is significant: material B is better.
1 Standard Deviation Test
We are trying to reduce the standard deviation of a critical dimension in order to improve the Cpk of its manufacturing process.
The previous standard deviation was 5 mm and after a process change we took a sample of 20 parts and obtained a standard deviation of 4 mm.
Has the process improved?
In sheet 1 Std Dev we start this analysis looking at the sample standard deviation confidence interval:
The previous standard deviation of 5 falls inside the interval so this means there is no significant improvement.
F Test for Two Variances
We want to compare two processes to choose the best one to reduce the variance of a critical dimension.
We have taken a sample of 31 parts from the original process and 42 parts of the new process and collected the variances in sheet 2Variances
We will use the F test for variances in Data Analysis:
1 Proportion Test
A soldering process has a 4% defect rate. We have changed some process parameters and we want to check if the process has improved.
To do this we took a sample of 100 products with the new process and found 2 defective.
Can we conclude that the process has improved?
In sheet 1Proportion we have checked with the confidence interval and then with the Z distribution:
The old rate 4% is inside the sample confidence interval so there is no significant improvement.
The p value 0.154 > 0.05 of the Z distribution also confirms this.
2 Proportion Test
We want to compare the quality level of two suppliers so we took a sample of parts from each and compared their defective rates.
In sheet 2Proportion we have analysed with confidence intervals and with the Z distribution:
Chi2 Test for Attributes
- Fail
- Marginal
- Pass
Defect Rate Comparisons
We have collected parts produced and defects every hour in sheet Defects
We want to see if defect rates are different on the different days of the week and the different shifts.
From the time stamps we can extract the DOW and Shift as done before:
The conclusion is that there is no significant differences in the defect rates of the different days of the week.
- Afternoon 1% average
- Morning 2%
- Night 3%
Lot Size Calculation
Now we want to find out what lot size do we need to run our analysis.
In our t distribution for analysis of means lot size will depend on:
- difference in mean we want to be able to detect δ
- process standard deviation σ
- α risk
- β risk
Conclusions
- Process data analysis enables decision taking based on significant statistical evidence rather than impressions
- The risk of making the wrong decision can be evaluated and it depends on the sample size analysed
- The sample size required when we use variables is much lower than using attributes
- Confidence intervals are useful graphic aids to interpret the results and make decisions
- Excel Data Analysis is a useful analysis tool
- Further analysis: Correlation, Regression and Design of Experiments























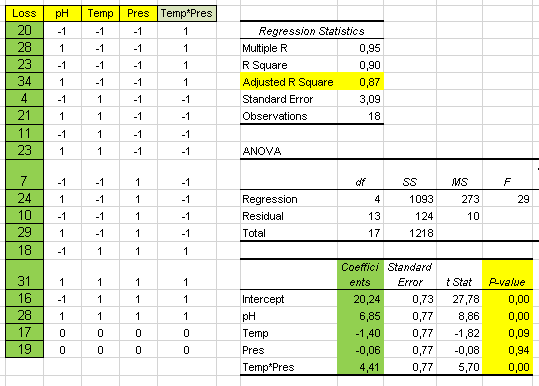
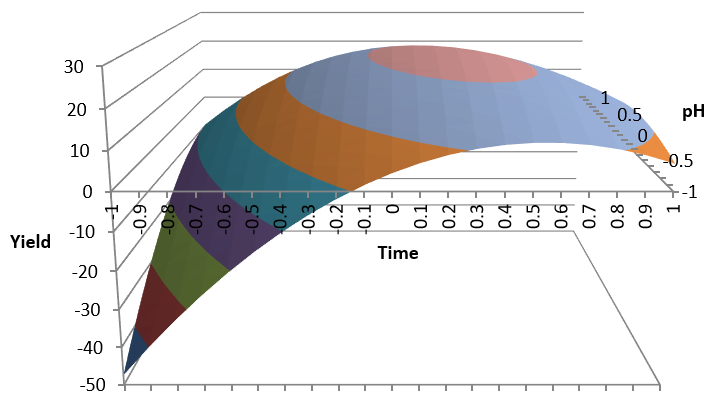

Comments
Post a Comment