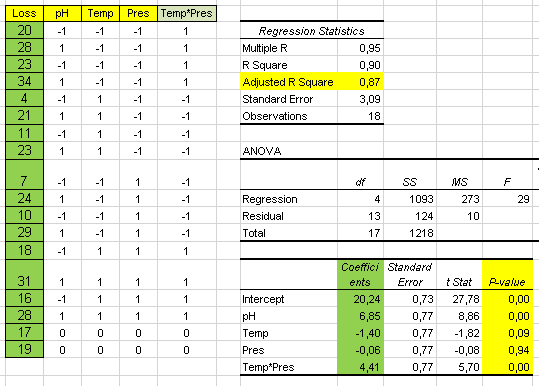
Test/ Repair Loop: Potential Value Stream Bottleneck

 

Test and Repair are Non-Value-Add operations: defective products should not be produced on the first place.

Unfortunately the state of the art in many processes is not there so tests and controls need to be part of the value stream. 


Ideally as the value stream becomes more robust some of these controls can be removed.

On the mean time we need a test and repair plan (if repair is possible).

A Test/ Repair loop can become a bottleneck for the whole Value Stream when Test First Pass Yield is lower than planned.

A drop in FPY is normally caused by problems upstream in the Value Stream as seen in

Test/ Repair loops are often absent in Value Stream Maps in spite of the potential to become the bottleneck for the total process.

Download this Excel example file  TestRepair.xlsm  to your PC from OneDrive folder  Polyhedrika

You must close all open Excel files before you open this one and you should enable Macros.




To simulate 1 hour operation just press F9. Press the RUN 100 button to run 100 cycles.

To reset (put all Work-In-Process to zero and set default values) press Ctrl + r

You can only write in the yellow cells.

This Test-Repair loop is part of a Value Stream with a Throughput of 100 units/ hour (Takt = 36 seconds) therefore you need to work out the minimum required Test and Repair capacities in order to deliver 100 units each hour.

This Excel file simulates a Test/ Repair loop such as:



Ideal Situation

The ideal case is when FPY = 100%. In this case no repair is necessary and the required test capacity is just 100, which corresponds to the Value Stream throughput.



Test FPY Drop

Let's assume 1% of the units are failing test: Test FPY = 99%:



The immediate result is that the output of this loop drops to 99: It has become the bottleneck of the Value Stream.

Since we are not repairing the faulty units, they are accumulating in front of the Repair station.

How much repair capacity do we need in this case?

All repaired items need to be retested so they will add to the new items entering the loop. What test capacity do we need then?

We can calculate this without the need for simulation:

In this case when we test 100 units only 99 come out OK (we have multiplied 100 by FPY which is 0.99).

If we need an output of 100 items OK how many do we need to test?

Answer: We divide by the FPY: 100/ 0.99 = 101.1 units per hour

And the repair capacity will be: 101.1 - 100 = 1.1 units per hour




Repair Time Variation

Test time typically doesn't have much variation, specially if it is automatic. Repair time, on the other hand, tends to have high variability. Some automatic testers may provide specific repair instructions but very often repair requires an investigation which might take a long time.

Let us assume that in our example an average repair capacity of 1.1 items/ hour has a standard deviation of 0.5:



The frequency distribution of this repair capacity will be:


And the result will be:




We see that occasionally output will drop and a queue will develop waiting for repair. This means we will need additional average repair capacity to compensate for this variation:




Now the "waiting for repair" queue has moved to "waiting for test" but it is not increasing and the output is maintained in 100.
 

Yield Drop Effects

Imagine that test FPY drops to 98% due to a problem upstream, maybe a supplier:




We have run 100 iterations pressing button   

We will need additional test capacity to test again the repaired units and also additional repair capacity.

The standard deviation of the test capacity will typically increase also and this will cause an accumulation of WIP both before test and before repair. This increase of WIP will increase the overall lead time of the Value Stream.
 

Non Repairable Units

We have assumed that all units may, eventually, be repaired but this is not always the case.

In case you have non-repairable units you can see the effect of yield loss on the value stream in:    Value Stream Constraints

Test/ Repair Loop in the Value Stream Map

The Test/ Repair loops should normally be included in the Value Stream Map because they are critical steps in the process which could become the bottleneck of the Value Stream. See an example in:    Excel Value Stream Map


Here we can see the effect of a Functional Test First Pass Yield of 80%:  
  • A 19%  additional repair and test capacity required to meet the takt time. 
  • And the side effect will be an accumulation of WIP of 13 units before repair and 66 units before test. 
  • This excess WIP will cause a 4 hour increase in leadtime.

Conclusions

  • A drop in Test FPY should trigger immediate actions to analyse and correct the source of the defects: avoid producing defects on the first place.
  • In the meantime we will need additional Test and Repair capacity to meet the value stream takt time.
  • The Repair operation may require high skills, which are typically in short supply, so enough training should be provided to insure it doesn't become the bottleneck for the total value stream.
  • By developing a robust Repair process we can reduce the average repair time and its standard deviation reducing this risk.
  • The repair operation should provide a Pareto of defects which could be traced back to their origin to avoid producing them on the first place. 
  • Test and Repair do not add value so the objective should be to reduce them and eventually discontinue them if possible.















Comments

Post a Comment

Popular posts from this blog

Design of Experiments (DOE) with Excel

Image
Design of Experiments (DOE) is a very useful process improvement methodology.  Microsoft Excel has some powerful data analysis tools, which I have, successfully, used for DOE. When it comes to analyzing cause and effect, we want to know what process factors affect our outputs.   Correlation and Regression could give us an indication of the main factors, and the extent they affect the outputs. In some cases, there may be interactions among the different factors, or the mathematical relation between factors and outputs may not be linear. In these cases, it is useful to run a systematic set of experiments, to test all possible combinations of factors, to relate them to the outputs. Factorial Experiment Example We want to minimize process loss, and after some brainstorming among the process specialists, we concluded that 5 factors may affect loss. Based on current factor levels, we have selected the following levels to experiment with:    Download this Excel file DOE_w...
Read more

Response Surface Design Of Experiments with Excel

Image
Design of Experiments is a useful methodology for process improvement. The purpose is to find a relationship between process variables we can control and key process outputs in order to increase process capability . You can use Excel statistical analysis tools, Solver, Pivot charts, etc. to plan and analyse the results of these experiments. The first approach is to look for a linear relationship as shown in:   Excel DOE But in some cases this relationship may not be linear, in which case we will try a quadratic model with Response Surface DOE . We will use an example in this Excel file you can download: Download file   ExcelResponseSurface.xlsm   from OneDrive to your PC. In this example we are trying to maximize process yield acting on the critical factors pH , Temperature and Time . We will run the experiments in the Experiments simulation sheet using coded values.   Code pH Temperature Time -1 2 120 7 1 12 150 15 Factorial Experiments We start by ru...
Read more

Virtual Obeya Room

Image
The Obeya room is a "war room" used by process improvement teams to meet and solve critical multi functional problems.  The room walls are lined up with boards, highly visual charts and graphs showing program timing, milestones and progress to date and countermeasures to existing timing or technical problems.  The team meets in this room regularly but team members can also visit the room, which is fully dedicated to the project, throughout the day. What is an Obeya? Obeya Room Benefits Remove organizational barriers Visual management by displaying all relevant data required in the improvement project Encourage a collaborative environment through regular meetings Implement quicker, more effective solutions The whole team knows what is going on in real time Some Practical Constraints in the Implementation Some companies can't afford the luxury of a fully dedicated room Some of the team members may be located far away so they will only attend the meetings The data displayed ...
Read more